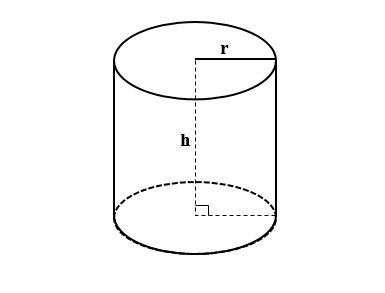
Công thức tính bán kính hình trụ
Xi lanh là gì? Làm cách nào để tính thể tích của hình trụ? Bài tập vận dụng công thức tính thể tích khối trụ được trình bày trong bài viết dưới đây.
1. một xi lanh là gì?
Hình trụ là hình có đáy là hình tròn song song và bằng nhau. Hình trụ được thể hiện trong hình bên dưới.
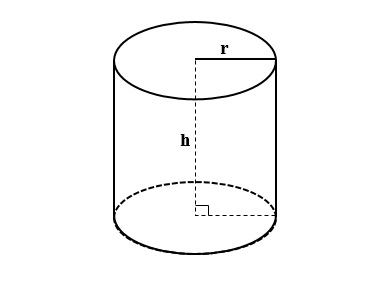
2. Công thức thể tích xi lanh
Thể tích của hình trụ bằng chiều cao nhân với bình phương bán kính đáy nhân với số pi. Hay thể tích hình trụ bằng diện tích đáy nhân với chiều cao.
Công thức thể tích xi lanh: v = sbottom.h = π.r2.h (m3)
Ở đâu:
- v là thể tích của hình trụ
- đáy là diện tích của đáy
- r là bán kính của hình tròn đáy
- h là chiều cao của hình trụ
- π là số pi, giá trị là 3,14
- Đơn vị thể tích là mét khối (m3)
- Đo đường kính của đáy và chia cho 2, vì d = 2r
- Nếu bạn biết chu vi của hình tròn đáy, hãy chia nó cho 2π, vì c = 2πr
- Đoạn thẳng nối hai tâm ở đáy hình trụ
- Đoạn thẳng nối một điểm trên đường tròn đáy và hình chiếu của nó trên một đường tròn đáy khác của hình trụ
2.1. Tìm bán kính đáy của hình trụ
Bạn có thể tìm bán kính đáy của một hình trụ bằng cách chỉ định bán kính của bất kỳ đường tròn nào cắt hình trụ và vuông góc với chiều cao. Bán kính của bất kỳ hình tròn nào như vậy bằng bán kính cơ sở. Bạn có thể tìm bán kính đáy của hình trụ bằng cách sử dụng:
2.2. Tính diện tích đáy của hình trụ
Khi biết giá trị của bán kính mặt đáy ta tính được diện tích mặt đáy của hình trụ theo công thức sau:
Diện tích đáy xi lanh: đáy = π.r2 (m2)
2.3. Tính chiều cao trụ
Chiều cao của hình trụ được định nghĩa là đoạn thẳng nối hai đáy và vuông góc với đáy của hình trụ. Vì vậy, có vô số đường thẳng là chiều cao của hình trụ và có hai vị trí quan trọng mà chiều cao có thể dễ dàng xác định:
Đặt thước vuông góc với mặt đáy và đọc kích thước của thước ở mặt đáy kia để biết chiều cao của hình trụ.
2.4. Diện tích đáy nhân với chiều cao
Sau khi tìm được diện tích đáy và chiều cao của hình trụ, ta nhân diện tích đáy với chiều cao để tìm thể tích của hình trụ. Bước này là bước cuối cùng trong quy trình tính toán thể tích xi lanh và là bước dễ dàng nhất.
3. Bài tập tính thể tích khối trụ
Bài tập 1: Chiều dài đáy của hình trụ là 30 cm và chiều cao là 10 cm. Thể tích của hình trụ này là bao nhiêu?
NGƯỜI CHIẾN THẮNG:
Bán kính đáy của hình trụ là: r = c/2π = 30/2.3,14 = 4,78 cm
Thể tích xi lanh: v = đáy.h = π.r2.h = 717,44 (cm3)
Đáp số: 717,44 (cm3)
Nhiệm vụ 2: Tính thể tích của hình trụ dưới đây, biết: r = 3 cm, ac = 5 cm.
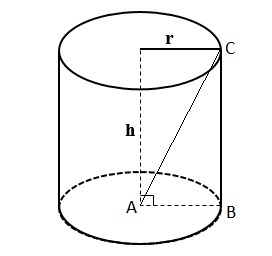
NGƯỜI CHIẾN THẮNG:
– Tính chiều cao của hình trụ:
Xét tam giác vuông abc, ta có:
ab = r = 3 cm
bc = h
bc2 = ac2 – ab2 = 52 – 32 = 16
=>BC = 4cm
=>Chiều cao = 4 cm
——tính diện tích đáy của hình trụ:
Đáy = π.r2 = 28,26 (cm2)
=>Thể tích của khối trụ trên là: v = đáy.h = 28,26,4 = 113,04 (cm3)
Vậy các em cần nhớ định nghĩa hình trụ và công thức tính thể tích hình trụ. Ngay cả những bài toán phức tạp liên quan đến thể tích của hình trụ cũng có thể giải được bằng công thức này. Điều quan trọng là tâm trí của bạn linh hoạt như thế nào. Việc làm nhiều bài tập sẽ giúp các em ghi nhớ công thức và rèn luyện kỹ năng giải tích các bài toán hình trụ. Chúc may mắn với toán học, đặc biệt là hình học!