Công thức nội suy Phương pháp nội suy 1 chiều, 2 chiều, tuyến tính. Nội suy được sử dụng rất phổ biến bởi các kỹ thuật viên. Dưới đây, chúng tôi tổng hợp các công thức và cách tính chi tiết nhất. Vui long tham khảo thông tin đo!
=>>>>Xem thêm: 999+ Trung Thu, stt Trung Thu 2022
i.Khái niệm nội suy
Nội suy là một phương pháp ước tính giá trị của một điểm dữ liệu chưa biết trong một tập hợp rời rạc gồm các điểm dữ liệu đã biết.
Trong khoa học kỹ thuật, người ta thường lấy mẫu các điểm dữ liệu có giá trị đã biết theo kinh nghiệm. Các điểm này là các giá trị đại diện của hàm biến độc lập với số giá trị hữu hạn. Thường thì chúng ta phải nội suy (hoặc ước lượng) giá trị của hàm này cho các giá trị trung gian của biến độc lập. Điều này có thể được thực hiện bằng cách sử dụng các phương pháp điều chỉnh đường cong hoặc phân tích hồi quy.
Phép nội suy là một công cụ toán học cơ bản được sử dụng rộng rãi trong nhiều ngành thử nghiệm như công nghệ thông tin, kinh tế, tài chính, dầu khí, xây dựng, y học, truyền hình, điện ảnh và nhiều ngành khác. Các ngành khác cần xử lý dữ liệu số…
ii, công thức nội suy 1 chiều
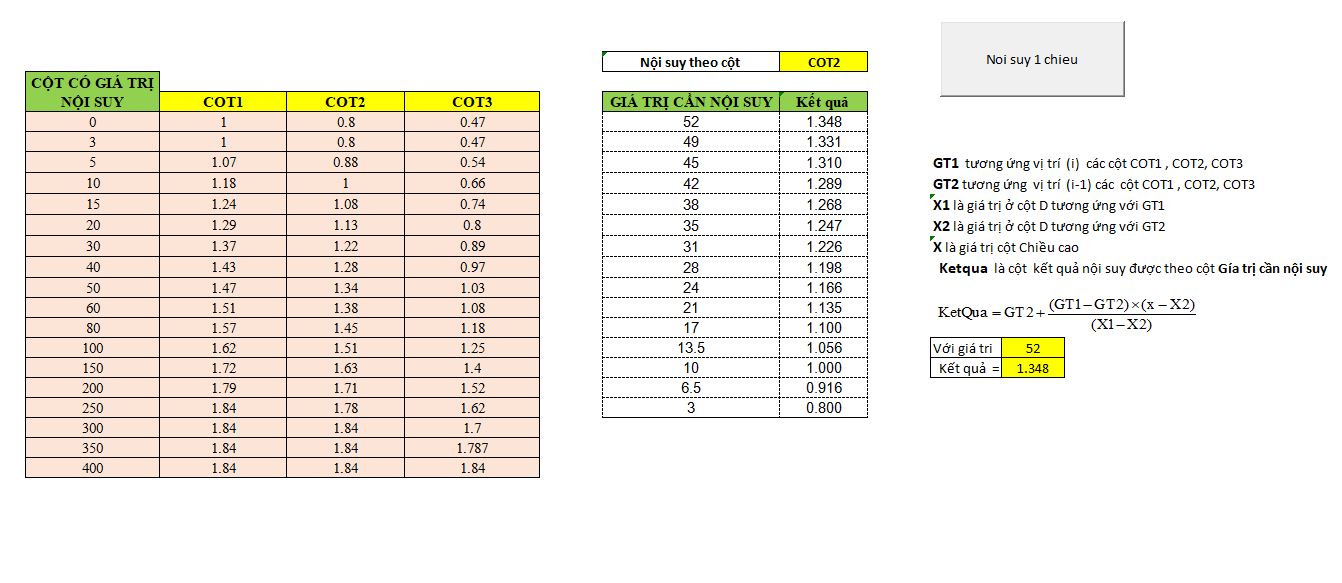
Ta có bảng sau:
b1: Tại ô nội suy cột, chọn cột tương ứng để nội suy (cot1, cot2, cot3)
Giá trị và mọi dữ liệu hiện có để chèn.
Công thức nội suy:
b2: hàm nội suy 1 chiều vba excel
+ câu lệnh if ….then (nếu…thì), câu lệnh là xét từ trái sang phải vị trí của cột được nội suy chính là cột trong bảng giá trị đã cho. (cot2 ở đây là cột thứ 3 tính từ trái sang phải trong bảng)
+ Sử dụng vòng lặp for để xác định phép nội suy.
Dựa trên công thức nội suy, chúng ta có một mô-đun nội suy

b3: Tạo nút lệnh để tự động tính toán.
Nhấp vào Nhà phát triển => Chèn => Nút lệnh để tạo nút lệnh
Nhấp đúp vào nút lệnh để nhập mã vba
<3
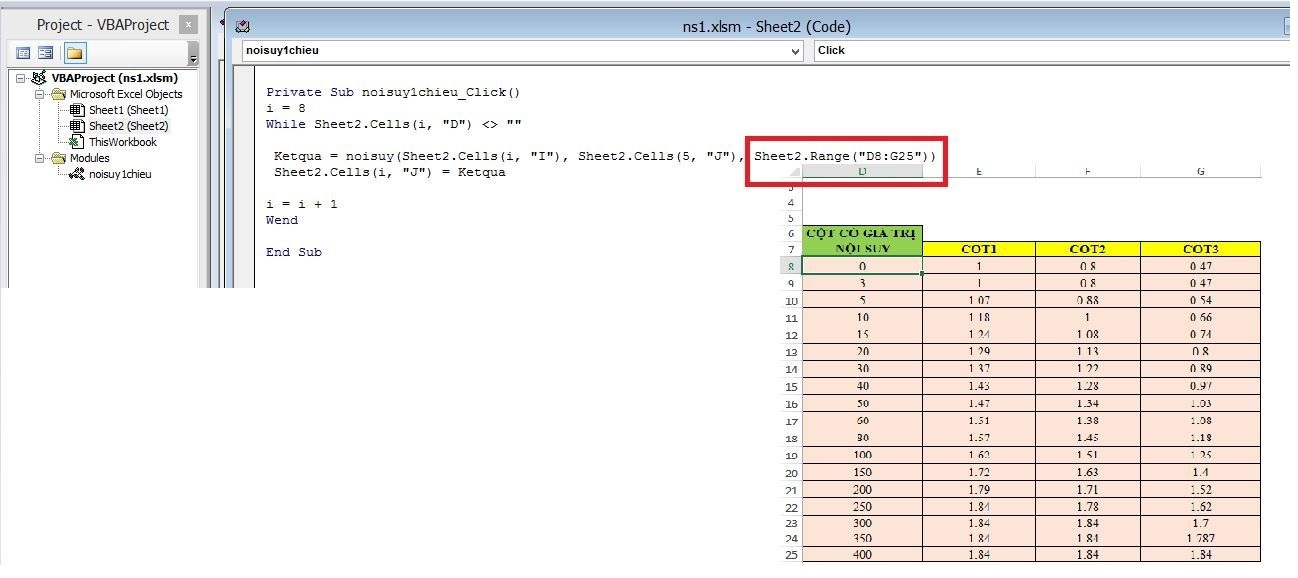
b4: Bấm vào nút lệnh mới để lấy kết quả nội suy
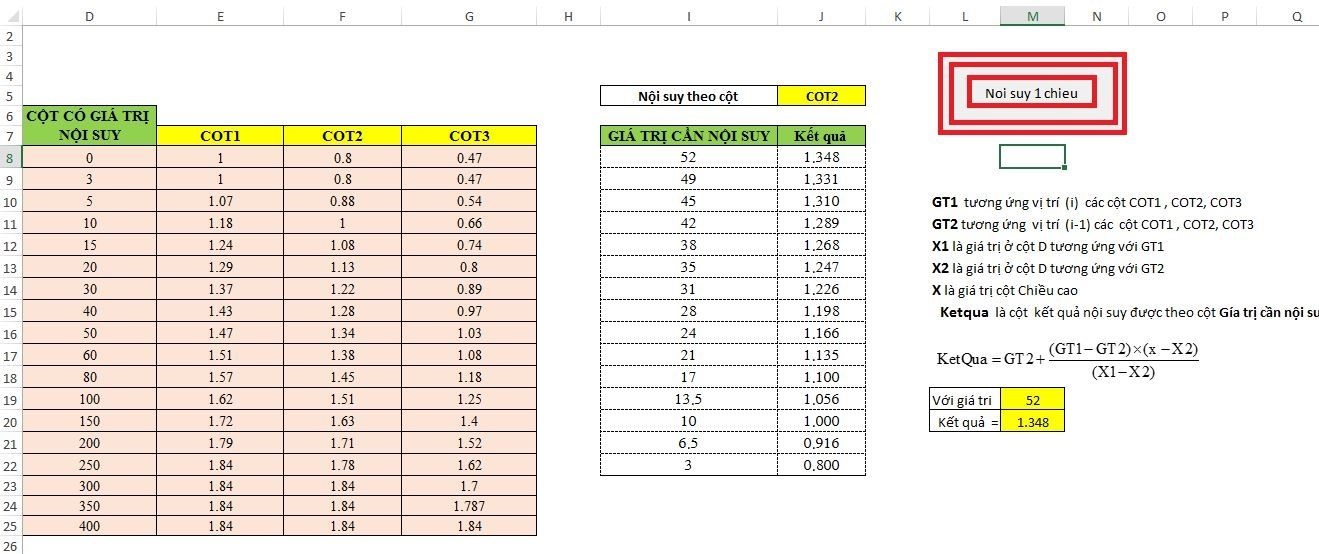
Tải xuống tệp nội suy 1D tại đây
iii, công thức nội suy 2 chiều
Ví dụ, chúng ta có bảng sau
Tạo một nút lệnh được tính toán tự động.
Nhấp vào Nhà phát triển => Chèn => Nút lệnh để tạo nút lệnh
Nhấp đúp vào nút lệnh để nhập mã vba
Bạn đã tạo một mô-đun
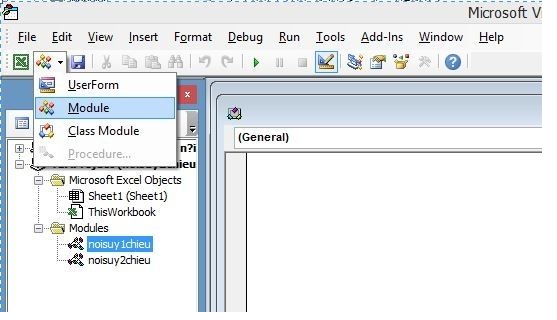
Đặt đoạn mã sau vào mô-đun
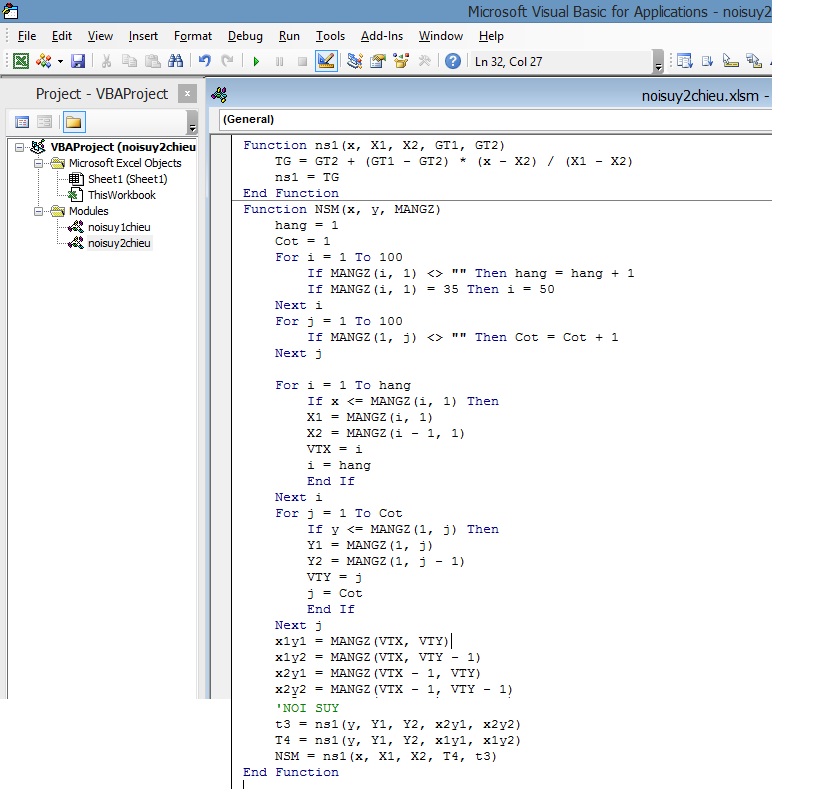
Tiếp tục với nút lệnh bạn vừa tạo, gõ đoạn mã sau vào đó
Lưu ý: nsm (giá trị cột 1, giá trị cột 2, vùng cần tra cứu)
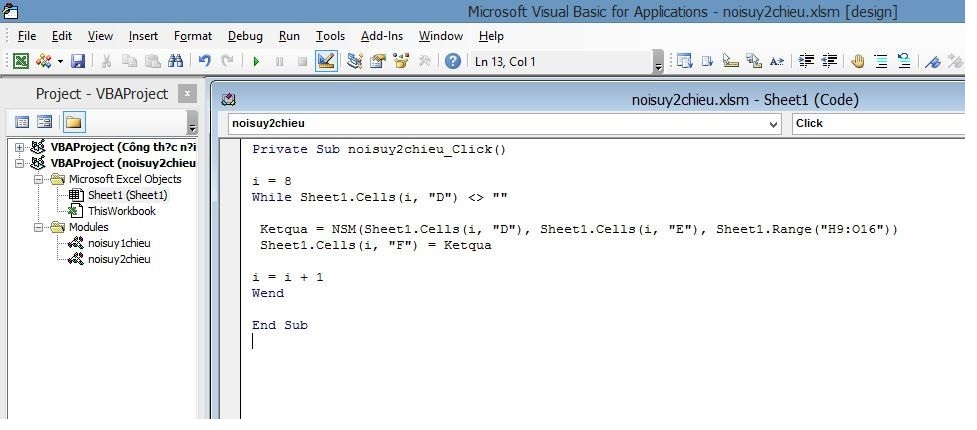
Nhấp vào nút lệnh nội suy 2D để chạy mã
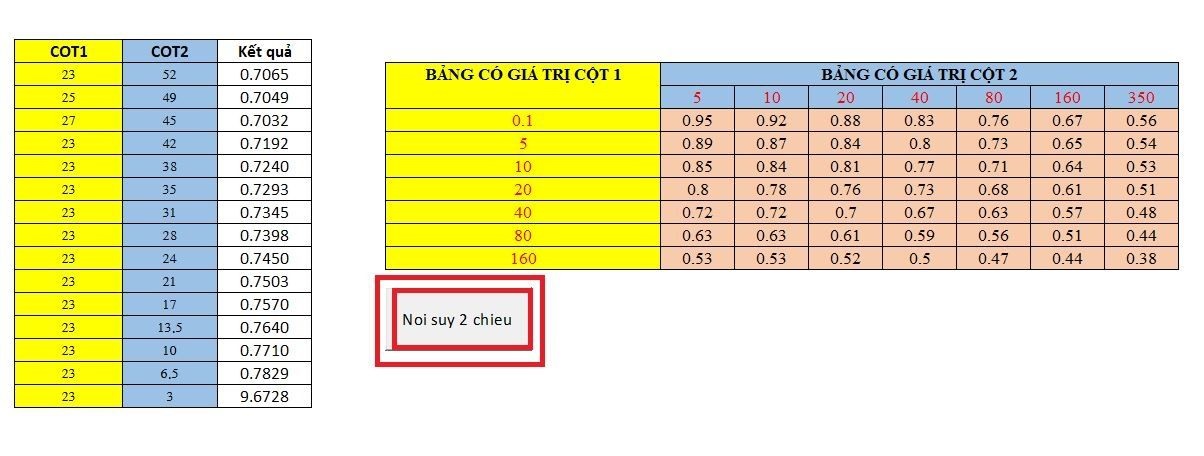
Tải xuống liên kết tới tệp ví dụ nội suy 2d tại đây
iv, nội suy tuyến tính
1.Nội suy tuyến tính là gì?
Nội suy tuyến tính là một quy trình cho phép bạn ngoại suy các giá trị giữa hai giá trị được xác định rõ, trong bảng hoặc trong biểu đồ tuyến tính.
Nội suy tuyến tính là một phương pháp bắt nguồn từ phương pháp nội suy tổng quát của Newton để xác định một giá trị chưa biết giữa hai số đã cho bằng cách xấp xỉ, nghĩa là có một giá trị trung gian. Nó cũng hoạt động đối với các hàm gần đúng, trong đó các giá trị của f(a) và f(b) đã biết và bạn muốn biết giá trị trung bình của f(x).
Có nhiều loại nội suy khác nhau như tuyến tính, bậc hai, bậc ba và cao hơn, đơn giản nhất là xấp xỉ tuyến tính. Chi phí của phép nội suy tuyến tính là kết quả sẽ không chính xác như phép tính gần đúng của hàm cấp cao hơn.
Ví dụ: nếu bạn biết rằng 3 lít sữa trị giá 4 đô la và 5 lít trị giá 7 đô la, nhưng bạn muốn biết 4 lít trị giá bao nhiêu, hãy nội suy để xác định giá trị trung bình tại thời điểm đó.
2.Phương pháp tính
Để ước lượng giá trị trung gian của hàm số, hàm f được xấp xỉ từ (x) đến đường thẳng r(x), tức là cho một đoạn “x = a” và “x = b”; nghĩa là, đối với (x0, x1) và (and0 , và 1) giá trị “x”, giá trị “y” được cho bởi đường nối giữa các điểm và được biểu thị bằng mối quan hệ sau:
(tổng – tổng 0) ÷ (x – x0) = (tổng 1 – tổng 0) ÷ (x1 – x0)
Để phép nội suy là tuyến tính, đa thức nội suy phải là bậc nhất (n = 1) để nó chia tỷ lệ tới các giá trị của x0 và x1.
Phép nội suy tuyến tính dựa trên sự đồng dạng của các tam giác, do đó, từ hình học trước, chúng ta có thể nhận được giá trị của “y”, đại diện cho giá trị chưa biết của “x”.
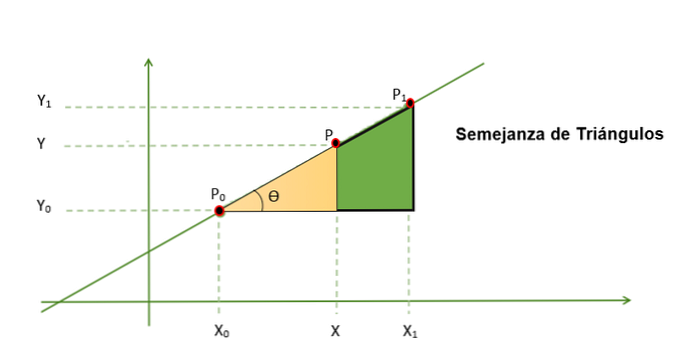
Sau đó, bạn phải:
a = tanƟ = (cạnh đối diện 1 cạnh kề 1) = (cạnh đối diện 2 cạnh kề 2)
Một cách diễn đạt khác là:
(tổng – tổng 0) ÷ (x – x0) = (tổng 1 – tổng 0) ÷ (x1 – x0)
Xóa biểu thức “và” và bạn có:
(tổng – tổng 0)*(x1 – x0) = (x – x0)*(tổng 1 – tổng 0)
(tổng – tổng 0) = (tổng 1 – tổng 0) * [(x – x0) ÷ (x1 – x0)]
Như vậy, chúng ta có được phương trình tổng quát cho phép nội suy tuyến tính:
y = y0 + (tổng 1 – tổng 0) * [(x – x0) ÷ (x1 – x0)]
Nói chung, có một lỗi nhỏ giữa phép nội suy tuyến tính và giá trị thực của hàm thực tế, mặc dù lỗi này rất nhỏ so với lựa chọn trực giác của bạn về một số gần với số bạn đang tìm kiếm.
Lỗi này xảy ra khi bạn cố gắng tính gần đúng giá trị của một đường cong bằng một đường thẳng; trong những trường hợp này, kích thước của khoảng phải được giảm xuống để làm cho giá trị gần đúng chính xác hơn.
Để có kết quả tốt hơn khi sử dụng phương pháp này, bạn nên sử dụng các hàm loại 2, 3 hoặc thậm chí cao hơn để thực hiện phép nội suy. Đối với những tình huống này, định lý Taylor là một công cụ rất hữu ích.
Ở trên là công thức nội suy một chiều, hai chiều và nội suy tuyến tính. Hi vọng bạn đã hiểu và áp dụng thành công. Lưu ý nhiều thông tin chung hữu ích khác được cập nhật chính xác tại https://noithattuephat.com/
Từ khóa tìm kiếm:
- Công thức nội suy
- Công thức nội suy một chiều
- Công thức nội suy tuyến tính
- Công thức nội suy Lagrange
- Công thức nội suy trong excel
- công thức nội suy excel
- Xây dựng công thức nội suy
- Nội suy trực tiếp
- Vấn đề nội suy
- Phương pháp nội suy
- Nội suy giữa hai điểm
- Chứng minh công thức nội suy
- Công thức nội suy cơ học đất