Công thức tính đường trung tuyến
Bạn có nhầm lẫn về công thức đường giữa không? Bạn lo lắng không biết công thức này áp dụng cho dạng toán nào? Đừng lo lắng, hãy theo dõi bài viết dưới đây của chúng tôi để biết thêm thông tin chi tiết. Chúng tôi sẽ tóm tắt những kiến thức về chủ đề này để bạn đọc dễ hiểu nhất có thể.
1. Công thức tính đường giữa
Đoạn thẳng đi qua trung điểm của đoạn thẳng gọi là trung trực của đoạn thẳng.
Đoạn thẳng kẻ từ đỉnh của tam giác đến trung điểm của cạnh đối diện gọi là trung tuyến của tam giác. Hãy chỉ ra rằng mọi tam giác đều đều có ba đường trung tuyến.
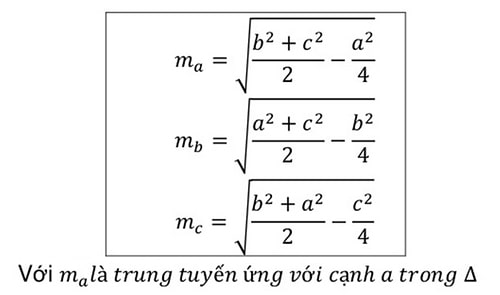
Đây là công thức chi tiết để tính chiều dài trung vị:
Công thức tính độ dài trung vị là căn bậc hai của một nửa tổng bình phương hai cạnh kề nhau. Sau đó trừ một phần tư bình phương của phía đối diện.
Công thức minh họa:
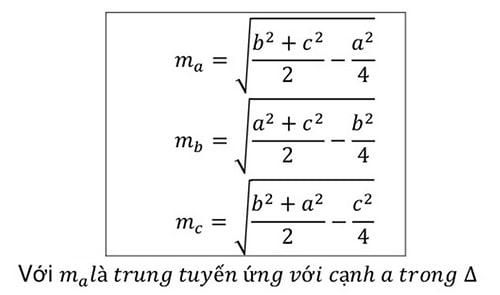
Ở đâu:
-
a, b, và c là các cạnh của tam giác.
-
ma, mb, mc lần lượt là đường trung tuyến của tam giác đó.
2. Tính chất đường trung tuyến của 3 tam giác đều, tam giác vuông và tam giác cân
Các đường trung tuyến trong mỗi tam giác sẽ có các thuộc tính khác nhau. Sau đây là tính chất cụ thể của từng tam giác.
Tam giác bằng nhau:
-
Trong một tam giác, giao điểm của ba đường trung tuyến được gọi là trọng tâm.
-
Trọng tâm của tam giác: Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến qua đỉnh đó.
Tam giác vuông:
-
Trung tuyến của tam giác vuông với cạnh huyền bằng một nửa cạnh huyền.
-
Tam giác vuông là tam giác có đường trung tuyến bằng một nửa độ dài cạnh.
Tam giác cân:
-
Trực tâm là đường trung trực kẻ từ đỉnh vuông góc với đáy tương ứng.
-
Đường phân giác là đường trung trực của góc chia góc đó thành 2 góc bằng nhau.
3. Bài tập minh họa
Bài tập 1: Tam giác mnp có np = 20 cm, pm = 16 cm, mn = 14 cm. Hãy tính độ dài đường trung tuyến của tam giác mnp.
Trang tính
Gọi:
-
np, pm, mn là a, b, c
-
ma, mb, mc lần lượt là độ dài trung tuyến của các đỉnh m, n, p của ∆mnp
.
Áp dụng công thức tính đường trung tuyến trong tam giác trên, ta có:
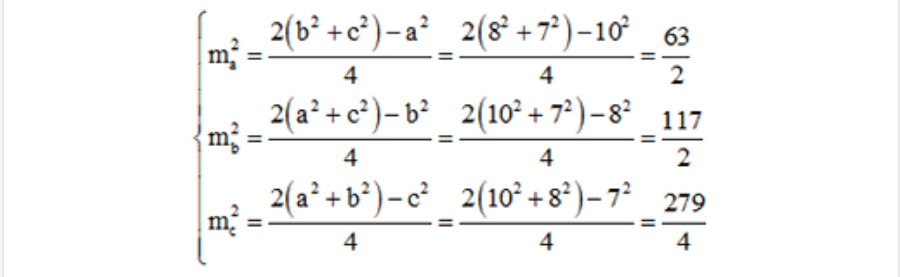
Vì độ dài đoạn thẳng là độ dài trung tuyến nên ta có:
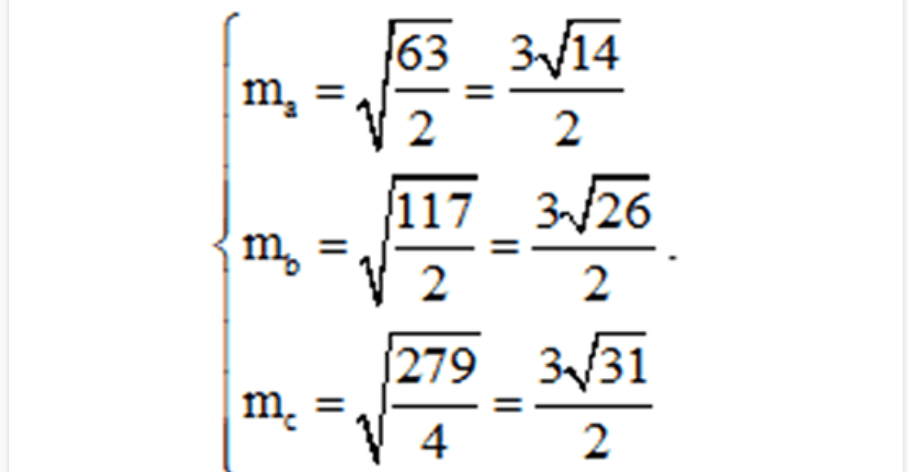
Bài tập 2: Cho tam giác mnp là tam giác cân tại m có mb = mc = 17cm và np = 16cm. Đường giữa mi.
a) Chứng minh: mi ⊥ np;
b) Tính độ dài mi.
Công việc:
A. đồ mi là đường giữa mnp
=> ip = tại
Mặt khác tam giác mnp cân tại m
=>mi vừa là trung tuyến vừa là cao độ
=> tối thiểu np
Ta có:
np = 16cm nên ni = pi = 8cm
mn = mp = 17cm
Xét tam giác vuông tại i
Áp dụng định lý Pitago, ta có:
mp2 = mi2 + ip2
=> 192= mi2 + 82
=> mi2 = 172 – 82 = 225
=> mi = 15cm.
Bài tập 3: Tam giác abc cân tại a, các trung tuyến be và cd cắt nhau tại g. Đoạn thẳng ag cắt bc tại điểm h. Vui lòng:
A. So sánh hai tam giác ahb và ahc.
m và n lần lượt là trung điểm của ga và gc. Chứng minh rằng an, be, cm đồng quy tại 1 điểm.
Công việc:
A. Chúng tôi có:
be và cd là hai đường trung tuyến của tam giác abc
Cắt cd tại g
=>Trọng tâm của tam giác abc là g
Nếu không thì bỏ qua g
=>Đường trung tuyến của tam giác abc là ah
Xét 2 tam giác ahb và ahc, có:
ab = ac
À Đại tướng
hb = hc
⇒ ahb = ahc(cạnh-cạnh-cạnh)
do ma = mg
=> cm là đường trung tuyến của tam giác agc (1)
khác ng = nc
=> an là đường trung tuyến của tam giác agc (2)
ge là trung tuyến của tam giác agc(3)
Từ (1), (2), (3) = > 3 đường thẳng an, cm, đồng quy.
Bài tập 4: Cho mk = mn cho tam giác mnk. Gọi e là giao điểm của hai trung tuyến ni và kp. Bằng chứng:
a) Tam giác nik và tam giác kpn đồng dạng
b) vi = ek
c) nk <;4ep
Công việc:
a) Ta có: mk=mn
ni là trung tuyến của tam giác mnk
=> ni = mn (1)
kp là đường trung tuyến của tam giác mnk
=>kp = mk (2)
Từ (1), (2) => ni=kp
Xét tam giác nik và tam giác kpn, ta có:
nk là lợi thế công cộng
ni = kp
Góc knp = góc nki (tam giác cân mnk tại m)
=> nik = kpn(cạnh-góc-cạnh)
b) Ta có:
góc mực = góc pkn (vì nik = kpn)
Vậy tam giác enk cân tại e
Suy ra en = ek
c) Xét mnk ta có:
im = ik (ni là trung tuyến)
pm = pn (kp là trung vị)
Suy ra ip là đường trung bình của tam giác mnk
=>ip=nk/2
Coi tam giác ipe là
ip
pe + ei (bất đẳng thức Cauchy)
pe = pk – ek
=>nk/2 < pk – ek + ei (3)
nik = Δkpn => kp = ni (4)
Tam giác enk tại e => là tam giác cân en = ek (5)
Từ (3), (4), (5) => nk/2 < ni – ne + ep
=>nk/2 < 2ep
=>nk < 4ep
Trên đây là thông tin về công thức trung vị. Hi vọng những chia sẻ trên có thể giúp các bạn thuận lợi hơn trong quá trình ôn thi.
-
-
-
-