Trong lớp mỹ thuật, em được học cách vẽ những bức tranh có đường nét cân đối, hài hòa. Những hình như vậy gọi là hình đối xứng. Trong chương trình toán học, các hình như hình tròn, hình chữ nhật, hình vuông,… cũng có tính chất đối xứng. Trong môn toán lớp 6, chúng ta học phép đối xứng tâm và phép đối xứng trục. Cụ thể, bài viết này sẽ giúp chúng ta hiểu về Trục đối xứng, hình có trục đối xứng và các dạng bài tập liên quan đến phép đối xứng. Mời các bạn theo dõi bài viết này!
Tôi. một trục đối xứng là gì?
Nhìn vào hình trên ta thấy đường thẳng a chia tam giác thành hai nửa bằng nhau (nếu gấp hình theo đường thẳng a thì hai nửa tam giác trùng nhau). Hình có thuộc tính này được gọi là hình có trục đối xứng và đường thẳng a được gọi là trục đối xứng.
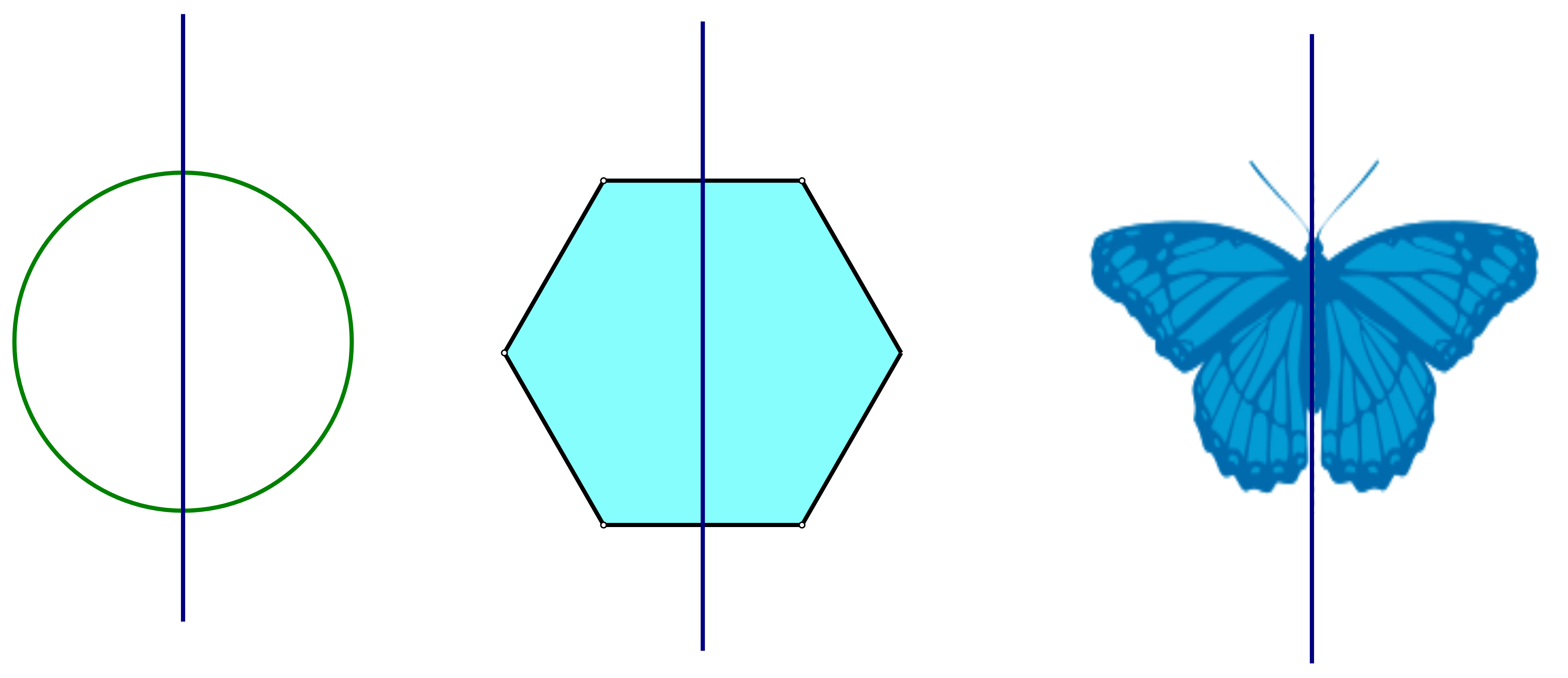
Ví dụ. Hãy xem những hình ảnh dưới đây và nhận xét những điểm chung của chúng.
Giải pháp.
Quan sát hình ta thấy các hình trên đều có một điểm chung đó là có một đường thẳng chia hình trên thành hai nửa, khi gấp hình theo đường thẳng này thì hai nửa đó trùng nhau .
*Lưu ý: Đối xứng trục còn được gọi là đối xứng trục.
Hai. Hình có trục đối xứng
1. Trục đối xứng của đoạn thẳng
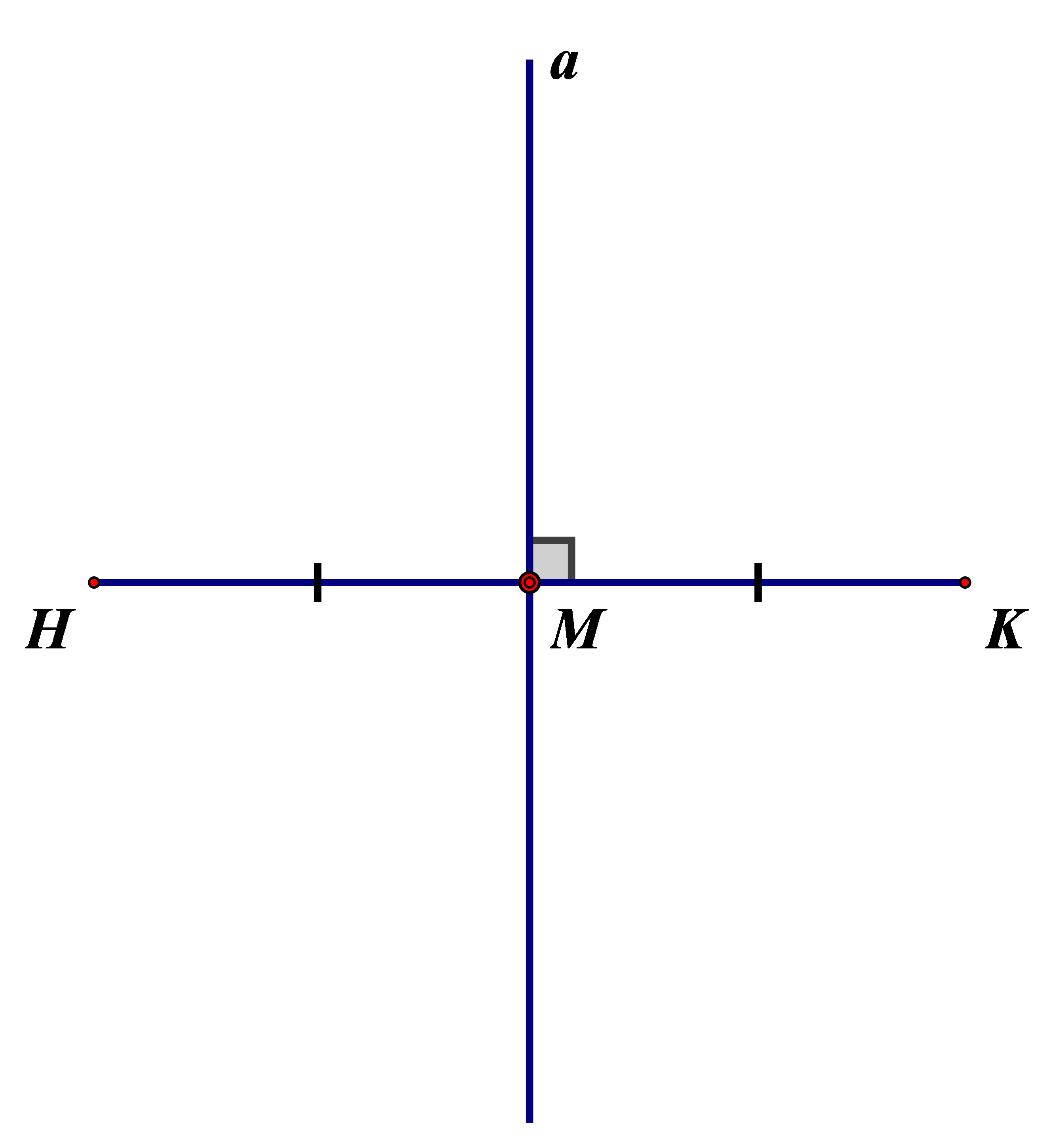
Trục đối xứng của đoạn thẳng hk là đường thẳng a đi qua trung điểm m của đoạn thẳng hk và vuông góc với hk. Khi đó đường thẳng a còn được gọi là đường trung trực của đường thẳng hk.
Ta cũng nói: điểm h và điểm k đối xứng nhau qua đường thẳng a.
2. Trục đối xứng của đường tròn
Trục đối xứng của đường tròn là đường thẳng đi qua tâm của đường tròn. Vậy đường tròn có vô số trục đối xứng.
3. Trục đối xứng của một số tam giác
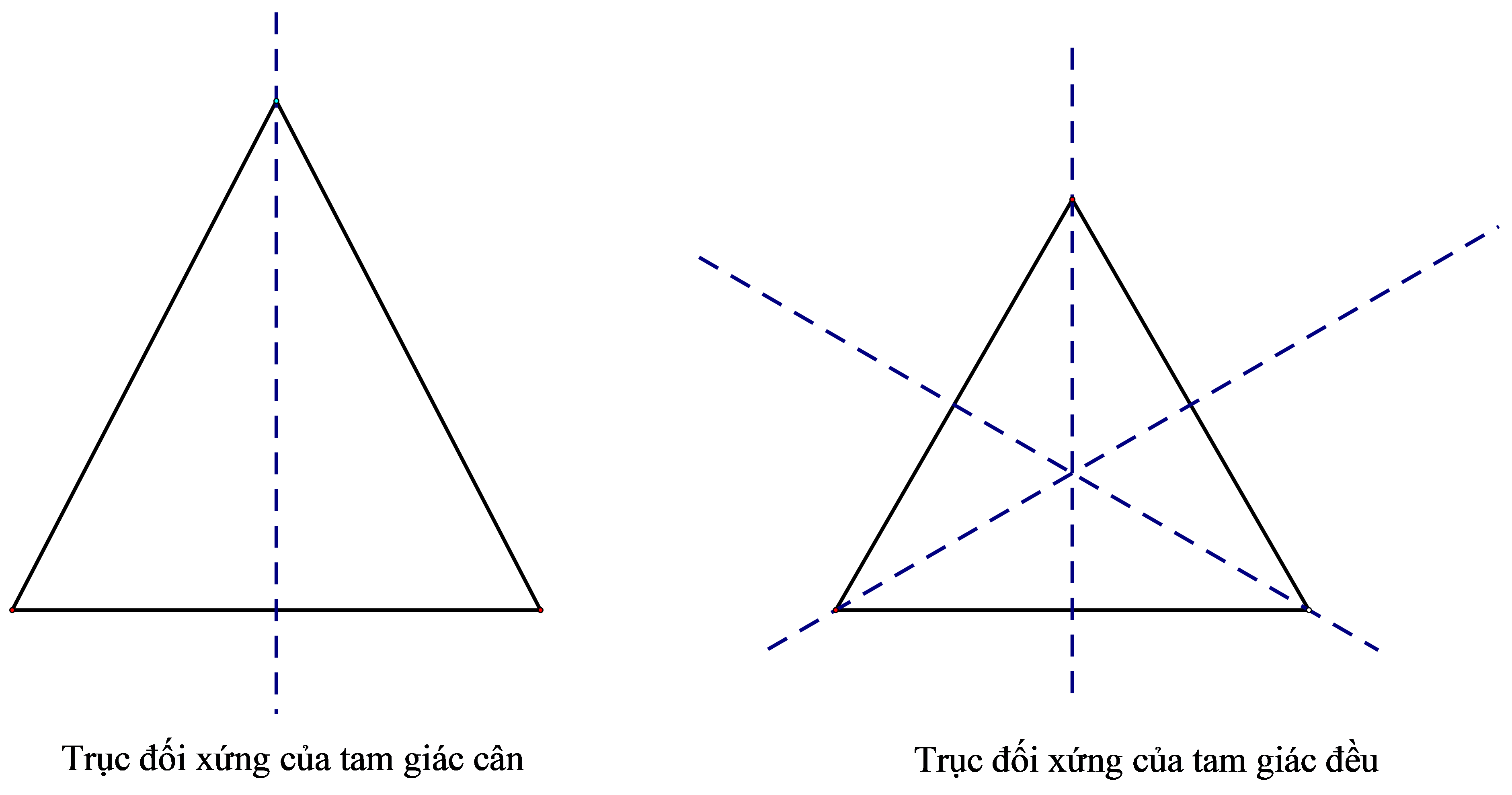
– Trục đối xứng của tam giác cân là đường thẳng đi qua các đỉnh và trung điểm của đáy tam giác cân, tam giác cân có một trục đối xứng.
– Các trục đối xứng của tam giác đều là các đường thẳng đi qua các đỉnh và trung điểm của các cạnh đối diện; tam giác đều có 3 trục đối xứng.
4. Trục đối xứng của một số tứ giác đều và lục giác đều
– Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm của hai đáy, hình thang cân có 1 trục đối xứng.
– Trục đối xứng của hình thoi là đường chéo của hình thoi và hình thoi có hai trục đối xứng.
– Trục đối xứng của hình chữ nhật là đường thẳng đi qua trung điểm của 2 cạnh đối diện, hình chữ nhật có 2 trục đối xứng.
– Các trục đối xứng của hình vuông là hai đường chéo của hình vuông và đường thẳng đi qua trung điểm của các cạnh đối diện; hình vuông có 4 trục đối xứng.
– Các trục đối xứng của lục giác đều là các đường thẳng đi qua các cặp đỉnh đối diện và các đường thẳng đi qua trung điểm của các cặp cạnh đối nên lục giác đều có 6 trục của sự đối xứng.
– Các trục đối xứng của ngũ giác đều là các đường thẳng đi qua các đỉnh và trung điểm của các cạnh đối diện; một ngũ giác đều có 5 trục đối xứng.

5. Trục đối xứng của một số chữ và số
Một số chữ và số có trục đối xứng, ví dụ: chữ a, b, m, y, h, x, o, số 3, 8, 0.
Ba. 6 dạng câu hỏi đối xứng trục
1. Dạng 1: Nhận biết hình phẳng có trục đối xứng dựa vào khái niệm trục đối xứng
*Phương pháp giải: Giải bài tìm hình có trục đối xứng theo khái niệm về trục đối xứng ở bài 1 và một số ví dụ về hình có trục đối xứng.
Nhiệm vụ 1.Điền câu trả lời thích hợp vào chỗ trống:
a) Đường thẳng đi qua hai đáy của hình thang cân là trục đối xứng của hình thang cân.
b) Hình thoi…là hai đường chéo của một hình thoi.
c) Đường tròn có trục đối xứng.
a) Đường thẳng đi qua trung điểm của hai đáy của hình thang cân là trục đối xứng của hình thang cân.
b) Trục đối xứng của hình thoi là hai đường chéo của hình thoi.
c) Đường tròn có vô số trục đối xứng.
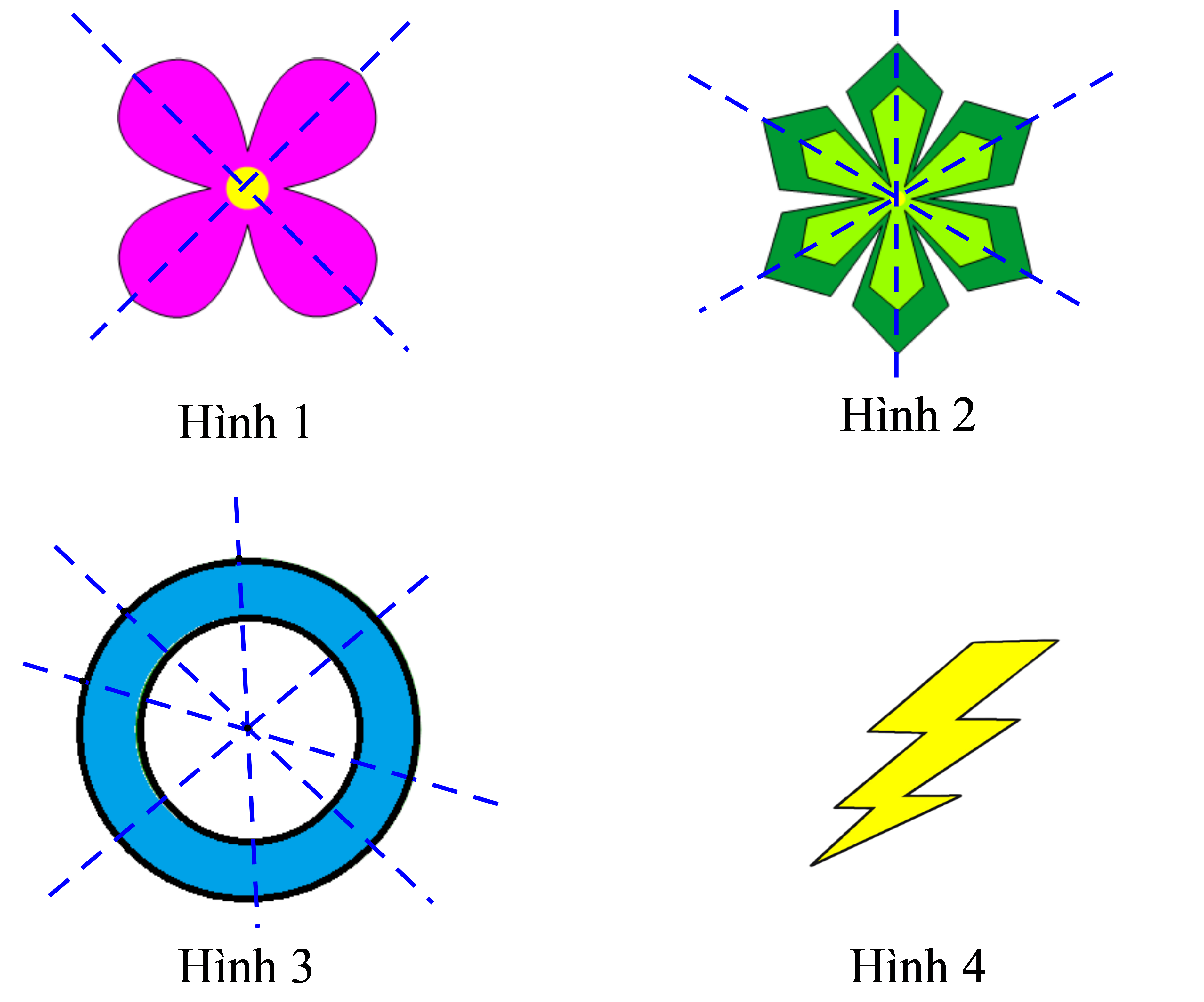
Bài giảng thứ haiHãy nhìn vào bức tranh bên dưới và trả lời các câu hỏi sau:

a) Hình nào không có trục đối xứng?
b) Hình nào có ba trục đối xứng?
c) Hình nào có vô số trục đối xứng?
Nhìn vào hình đã cho, ta thấy:
a) Đồ thị không có trục đối xứng là: Hình 4.
b) Hình đối xứng ba trục là: Hình 2
c) Đồ thị có vô số trục đối xứng là: Hình 3.
2.Dạng 2: Áp dụng phép đối xứng trục cho ảnh thật
*Lời giải: Trục đối xứng có nhiều ứng dụng, giúp miêu tả hình ảnh một cách hài hòa, cân đối. Dựa vào khái niệm đối xứng trục trong hình học minh họa các hình trong đời thực đều có tính chất đối xứng trục.
Tập thể dục. Nhìn vào những bức ảnh kiến trúc và nghệ thuật dưới đây, hình nào có trục đối xứng?

Các hình có trục đối xứng được thể hiện trong Hình 1 và Hình 3.

Do đó, bài viết này tổng hợp kiến thức về ảnh có trục đối xứng. Đây là điều cơ bản và có nhiều ứng dụng trong đời sống thực tế. Vì vậy, các em cần nắm vững kiến thức về trục đối xứng để học tốt các khóa học sau và vận dụng vào cuộc sống hàng ngày.
Người phụ trách nội dung: Cô giáo Nguyễn Thị Trang
